Counting Rules
Whether we want to find out in how many ways can a coach select 4 forward soccer players from a group of 7 players; or how many groups of 6 numbers can be randomly drawn from a collection of 49 different numbers; or in how many ways can 10 trees be planted, counting (combinatorial) methods can help extraordinarily. The following sections present basic counting rules and cases.
The Product Rule (The Principle of Multiplication )
Consider two experiments where the first one produces j outcomes and the second one results in k outcomes. If you combine the two experiments so that each outcome of the first experiment comes up with each outcome of the second experiment then there will be a total of j · k [paired] outcomes. One can extend this rule to more than 2 experiments. The total number of outcomes of m experiments, each having ni, i = 1, 2, ..., m , possible outcomes (simple events) is equal 
n1 · n2 · ... · nm.
Example - Product Rule:
Combined experiments of Flipping a Fair Coin, with Sample Space {H, T}, and Rolling a Fair Die with Sample Space {1, 2, 3, 4, 5, 6}, have 2 · 6 = 12 outcomes (simple events). Each side (H, T) of the coin is combined with each number of the die (1, 2, 3, 4, 5, 6).
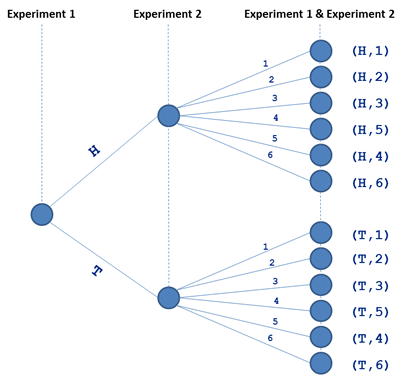
This multiplication syndrome can also be visualized as a tree, where nodes represent experiments and branches symbolize simple events.
If H comes out in the first experiment, it can be followed by any of the 6 numbers of the second experiment. The same can be said about the T outcome of the first experiment.
It is easy to learn from the tree why this multiplication rule works. As expected, the leaves of the tree show all possible arrangements of the outcomes (simple events) of the experiments. They constitute the Sample Space of the combined experiments, S = { (H,1), (H,2), (H,3), (H,4), (H,5), (H,6), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6) }.
If we were interested in assessing the probability of Heads (H) combined with an odd number to come out we would notice that 3 out of 12 simple events, {(H,1), (H,3), (H,5)} satisfy such an event. Thus the probability of this event would be 3/12 = 1/4.
Tree
Full-set Permutations
In how many ways can a set of n elements be arranged in terms of the order of the elements? The total number of such arrangements (permutations) is equal to:.
Pn = 1 · 2 · ...· n = n!
Notation n! is an n factorial. One element (a) can be arranged in 1 way, {(a)}, P1 = 1. Adding a second element (b) will double the number of the arrangements {(ab), (ba)}, P2 = 1·2. A third element (c) will triple the number of already existing arrangements {(cab), (acb), (abc), (cba), (bca), (bac)} , P3 = 1·2·3, etc.
Example - Full-set Permutations:
In how many ways can be letters of word "GOLF" be arranged. Since word GOLF consists of n = 4 letters, the number of the permutations is n! = 5!= 120.
# R Code
n = 4
factorial(n)
[1] 24
How can we visualize these permutations (arrangements)? There is a package called "combinat" the can help us. First, we need to install it. Next, the package (library) is to be opened.
# Add package "combinat" to R.
install.packages("combinat")
# Open package "combinat".
library(combinat)
# Define word GOLF.
word = "GOLF"
word
[1] "GOLF"
# We will use function permn of library combinat to list all [full-set] permutations
# of a set of characters contained in string word.
# Since function perm deals with vectors of elements, we need to convert string "GOLF"
# to a vector of characters. To this end we can use function split (built-in R) which
# returns a list object.
lword = strsplit(word, "")
lword
[[1]]
[1] "G" "O" "L" "F"
# We got a list consisting of one element (recall that list elements are accessed
# using the double-bracket notation. We can retrieve the first element as a vector
# by using index 1 of the list ([[1]]).
vword = lword[[1]]
vword
[1] "G" "O" "L" "F"
# Having our word represented as a vector word (vword), we can use it
# to generate all possible [full-set] permutations of the vword set (vector).
pwords_aslist = permn(vword)
pwords_aslist
[[1]]
[1] "G" "O" "L" "F"
[[2]]
[1] "G" "O" "F" "L"
[[3]]
[1] "G" "F" "O" "L"
[[4]]
[1] "F" "G" "O" "L"
[[5]]
[1] "F" "G" "L" "O"
[[6]]
[1] "G" "F" "L" "O"
[[7]]
[1] "G" "L" "F" "O"
[[8]]
[1] "G" "L" "O" "F"
[[9]]
[1] "L" "G" "O" "F"
[[10]]
[1] "L" "G" "F" "O"
[[11]]
[1] "L" "F" "G" "O"
[[12]]
[1] "F" "L" "G" "O"
 Continuation
[[13]]
[1] "F" "L" "O" "G"
[[14]]
[1] "L" "F" "O" "G"
[[15]]
[1] "L" "O" "F" "G"
[[16]]
[1] "L" "O" "G" "F"
[[17]]
[1] "O" "L" "G" "F"
[[18]]
[1] "O" "L" "F" "G"
[[19]]
[1] "O" "F" "L" "G"
[[20]]
[1] "F" "O" "L" "G"
[[21]]
[1] "F" "O" "G" "L"
[[22]]
[1] "O" "F" "G" "L"
[[23]]
[1] "O" "G" "F" "L"
[[24]]
[1] "O" "G" "L" "F"
# We got the permutations but they are inconveniently shown as a list of vectors.
# To convert the list to a vector of words (string) we need to first convert
# each element (vector) of the list to a string and then also convert the list
# itself to a vector. The first job can be done, using function paste that
# concatenates elements. We will first do it in classic way by traversing the
# list and converting each of its elements to a string.
n = length(pwords_aslist)
for (i in 1:n) {
  pwords_aslist[[i]] = paste(pwords_aslist[[i]], sep='',collapse='')
}
pwords_aslist

[[1]]
[1] "GOLF"
[[2]]
[1] "GOFL"
[[3]]
[1] "GFOL"
[[4]]
[1] "FGOL"
[[5]]
[1] "FGLO"
[[6]]
[1] "GFLO"
[[7]]
[1] "GLFO"
[[8]]
[1] "GLOF"
[[9]]
[1] "LGOF"
[[10]]
[1] "LGFO"
[[11]]
[1] "LFGO"
[[12]]
[1] "FLGO"
Continuation
[[13]]
[1] "FLOG"
[[14]]
[1] "LFOG"
[[15]]
[1] "LOFG"
[[16]]
[1] "LOGF"
[[17]]
[1] "OLGF"
[[18]]
[1] "OLFG"
[[19]]
[1] "OFLG"
[[20]]
[1] "FOLG"
[[21]]
[1] "FOGL"
[[22]]
[1] "OFGL"
[[23]]
[1] "OGFL"
[[24]]
[1] "OGLF"
# Next, we need to convert this ugly output (list - pwords_aslist) to a more
# compact one (vector - pwords).
pwords = unlist(pwords_aslist)
pwords
[1] "GOLF" "GOFL" "GFOL" "FGOL" "FGLO" "GFLO" "GLFO" "GLOF" "LGOF" "LGFO"
[11] "LFGO" "FLGO" "FLOG" "LFOG" "LOFG" "LOGF" "OLGF" "OLFG" "OFLG" "FOLG"
[21] "FOGL" "OFGL" "OGFL" "OGLF"
# As we all know, R provides many opportunities for solving the same problem.
# Also, in this case we can do think differently, probably -- better.
# The above conversion of the list vector-elements to the string-elements
# can be simplified. However, we need a specialized function to convert
# a vector to a string. Notice that the above paste function uses three
# argument: s, sep, and collapse. The last two are fixed. They do not change
# inside of the above for loop. We can define our own function that will
# take only one argument (the list itself) and return a string, using the other
# arguments being set to an empty string (by default). Let's call this function
# pasteSpecial.
pasteSpecial = function(s) {
  return ( paste(s,sep='',collapse='') )
}
# We can now replace the for loop with a [cool] repetitive function lapply
# (apply a function to a list).
pwords_aslist = lapply(pwords_aslist,pasteSpecial)
pwords_aslist
[[1]]
[1] "GOLF"
[[2]]
[1] "GOFL"
[[3]]
[1] "GFOL"
[[4]]
[1] "FGOL"
[[5]]
[1] "FGLO"
[[6]]
[1] "GFLO"
[[7]]
[1] "GLFO"
[[8]]
[1] "GLOF"
[[9]]
[1] "LGOF"
[[10]]
[1] "LGFO"
[[11]]
[1] "LFGO"
[[12]]
[1] "FLGO"
 Continuation
[[13]]
[1] "FLOG"
[[14]]
[1] "LFOG"
[[15]]
[1] "LOFG"
[[16]]
[1] "LOGF"
[[17]]
[1] "OLGF"
[[18]]
[1] "OLFG"
[[19]]
[1] "OFLG"
[[20]]
[1] "FOLG"
[[21]]
[1] "FOGL"
[[22]]
[1] "OFGL"
[[23]]
[1] "OGFL"
[[24]]
[1] "OGLF"
The above procedure can be conveniently wrapped in a UDF (user-defined function). Such a function receives a string of character, word, to return a vector of the [full-set] permutations. Notice that function pasteSpecial is repeated here for convenience.
pasteSpecial = function(s) {
  return ( paste(s,sep='',collapse='') )
}

fullSetPermutations = function(word) {
  n = nchar(word)
  lword = strsplit(word, "")
  vword = lword[[1]]
  pwords_aslist = combinat::permn(vword)
  pwords_aslist = lapply(pwords_aslist,pasteSpecial)
  return ( unlist(pwords_aslist) )
}
# Let's use this function to generate all [full-set] permutations of all the characters in string "ABC".
fullSetPermutations("ABC")
[1] "ABC" "ACB" "CAB" "CBA" "BCA" "BAC"
Notice that notation combinat::permn(vword) is a shortcut for getting function permn from library combinat.
 
Subset Permutations
A generalization of the full-set permutations is a sub-set permutations. Here, we want to generate or count the number of permutations of k-elements selected from a set of
n-elements. For example, in how many ways one can arrange 3 digits selected from the set of 5 digits, {1,2,3,4,5}:
{1,2,3}, {2,1,3}, {3,1,2}, {3,2,1}, {2,3,4}, etc.
This problem can be solved manually (a tedious one) or programmatically, using R library "iterpc". Let's first do the counting (an easier task).
# R Code
n = 5
m = 3
factorial(n)/factorial(n-m)
[1] 60
Notice that the full-set permutation count is just factorial(5) = 120. In our case each of the permutations "ignores" 2 digits. Let's use our partial (manual) list to compare the m-element permutations with a few of the n-element ones.
{1,2,3}{1,2,3,4,5}
{1,2,3,5,4}
{2,1,3}{2,1,3,4,5}
{2,1,3,5,4}
{3,1,2}{3,1,2,4,5}
{3,1,2,4,5}
{3,2,1}{3,2,1,4,5}
{3,2,1,4,5}
{2,3,4}{2,3,4,1,5}
{2,3,4,1,5}
Etc.
We can see that the number of the full-set permutations is reduced (n - m) = ( 5-3) = 2 times. This is why the general formula for the m-element permutations selected from the
n-element set is:
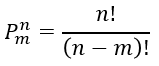
Subset Permutations
Let's use the iterpc library to visualize subset permutations.
# Add package "iterpc" to R.
install.packages("iterpc")
# Open package "iterpc".
library(iterpc)
# Show all 3 element subsets selected from 5-digit data set {1,2,3,4,5}.
i = iterpc(5, 3, ordered=TRUE)
getall(i)
      [,1] [,2] [,3]
 [1,]    1    2    3
 [2,]    1    2    4
 [3,]    1    2    5
 [4,]    1    3    2
 [5,]    1    3    4
 [6,]    1    3    5
 [7,]    1    4    2
 [8,]    1    4    3
 [9,]    1    4    5
[10,]    1    5    2
[11,]    1    5    3
[12,]    1    5    4
[13,]    2    1    3
[14,]    2    1    4
[15,]    2    1    5
 Continuation
[16,]    2    3    1
[17,]    2    3    4
[18,]    2    3    5
[19,]    2    4    1
[20,]    2    4    3
[21,]    2    4    5
[22,]    2    5    1
[23,]    2    5    3
[24,]    2    5    4
[25,]    3    1    2
[26,]    3    1    4
[27,]    3    1    5
[28,]    3    2    1
[29,]    3    2    4
[30,]    3    2    5
 Continuation
[31,]    3    4    1
[32,]    3    4    2
[33,]    3    4    5
[34,]    3    5    1
[35,]    3    5    2
[36,]    3    5    4
[37,]    4    1    2
[38,]    4    1    3
[39,]    4    1    5
[40,]    4    2    1
[41,]    4    2    3
[42,]    4    2    5
[43,]    4    3    1
[44,]    4    3    2
[45,]    4    3    5
 Continuation
[46,]    4    5    1
[47,]    4    5    2
[48,]    4    5    3
[49,]    5    1    2
[50,]    5    1    3
[51,]    5    1    4
[52,]    5    2    1
[53,]    5    2    3
[54,]    5    2    4
[55,]    5    3    1
[56,]    5    3    2
[57,]    5    3    4
[58,]    5    4    1
[59,]    5    4    2
[60,]    5    4    3
We can also map digital elements to text elements and show the output as text. Suppose we want to form all arrangements of 2 letter subsets selected from a letter set {A,B,C}.
Notice that variable LETTERS is a built-in vector. It contains all capital letters of the basic latin alphabet. Expression LETTERS[1:3] stand for the 3 first letters.
i = iterpc(3, 2, labels=LETTERS[1:3], ordered=TRUE)
getall(i)
    [,1] [,2]
[1,] "A"  "B"
[2,] "A"  "C"
[3,] "B"  "A"
[4,] "B"  "C"
[5,] "C"  "A"
[6,] "C"  "B"
Also in this case we can wrap this procedure for getting the subset-permutations in an UDF. It is assumed that the function is getting the text input set (txtset), and the size, m, of the permutations. For convenience the definition of the pasteSpecial function is repeated here.
pasteSpecial = function(s) {
  return ( paste(s, sep='',collapse='') )
}
subSetPermutations = function(txtset, k) {
  lst = strsplit(txtset, "")
  v = lst[[1]]
  n = length(v)
  i = iterpc::iterpc(n, m, labels=v, ordered=TRUE)
  matp = iterpc::getall(i)
  return ( apply(matp,MARGIN=1,pasteSpecial) )
}
# Let's use this function to generate all sub-set permutations of the 3 characters in string "ABCD".
subSetPermutations("ABCD",3)
 [1] "ABC" "ABD" "ACB" "ACD" "ADB" "ADC" "BAC" "BAD"
 [9] "BCA" "BCD" "BDA" "BDC" "CAB" "CAD" "CBA" "CBD"
[17] "CDA" "CDB" "DAB" "DAC" "DBA" "DBC" "DCA" "DCB"
Notice that notation iterpc:: is a shortcut for library iterpc.
Example - Subset Permutations:
In how many ways can letters of word "bookkeeper" be rearranged? Note that bookkeeper is the same permutation as bookkeeper.
There are the following counts of repeated letters in this word:
e 3
k 2
o 2
Since rearrangements of the same letter should be ignored, the total number of permutations
of the letters in "bookkeeper" is:
# Input:
word = "bookkeeper"
en = 3
kn = 2
on = 2
# Processing:
n = nchar(word)
cnt = factorial(n)/( factorial(en) * factorial(kn) * factorial(on) )
# Output:
cnt
[1] 151200
There are 151,200 permutations of the letters in "bookkeeper".
A 10-letter word with all unique letters has the following number of permutations.
factorial(10)
[1] 3628800
This is 24 (6·2·2) times higher than the number of the permutation of "bookkeeper".
 
Combinations
Combinations of k elements selected from a set of n elements are arrangements of the elements where all their permutations of the same elements are representing one combination. For example, permutations {a,b,c}, {a,c,b}, {b,a,c}, {b,c,a}, {c,a,b}, {c,b,a} are reduced to just one combination {a,b,c}. The number of such combinations is given by the following formula:
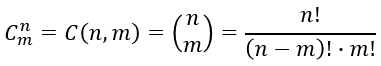
Combinations
Comparing it to the formula for the subset permutations, we notice that the number of the combination is m! times smaller (since all of the m-element permutations are mapped to just one combination).
Why don't we first develop another UDF to show combinations. Let's use function combn of library utils (if necessary run install.packages("utils") before completing the following case.
pasteSpecial = function(s) {
  return ( paste(s,sep='',collapse='') )
}
combs = function(txtset, m) {
  lst = strsplit(txtset, "")
  v = lst[[1]]
  matc = utils::combn(v, m, simplify = TRUE)
  return ( apply(matc,MARGIN=2,pasteSpecial) )
}
Now, to visualize how this works, consider first full set permutations of the 5-letter set ("ABCDE").
# The number of the permutations.
factorial(5)
[1] 120
# The permutations.
fullSetPermutations("ABCDE")
  [1] "ABCDE" "ABCED" "ABECD" "AEBCD" "EABCD" "EABDC" "AEBDC" "ABEDC" "ABDEC"
 [10] "ABDCE" "ADBCE" "ADBEC" "ADEBC" "AEDBC" "EADBC" "EDABC" "DEABC" "DAEBC"
 [19] "DABEC" "DABCE" "DACBE" "DACEB" "DAECB" "DEACB" "EDACB" "EADCB" "AEDCB"
 [28] "ADECB" "ADCEB" "ADCBE" "ACDBE" "ACDEB" "ACEDB" "AECDB" "EACDB" "EACBD"
 [37] "AECBD" "ACEBD" "ACBED" "ACBDE" "CABDE" "CABED" "CAEBD" "CEABD" "ECABD"
 [46] "ECADB" "CEADB" "CAEDB" "CADEB" "CADBE" "CDABE" "CDAEB" "CDEAB" "CEDAB"
 [55] "ECDAB" "EDCAB" "DECAB" "DCEAB" "DCAEB" "DCABE" "DCBAE" "DCBEA" "DCEBA"
 [64] "DECBA" "EDCBA" "ECDBA" "CEDBA" "CDEBA" "CDBEA" "CDBAE" "CBDAE" "CBDEA"
 [73] "CBEDA" "CEBDA" "ECBDA" "ECBAD" "CEBAD" "CBEAD" "CBAED" "CBADE" "BCADE"
 [82] "BCAED" "BCEAD" "BECAD" "EBCAD" "EBCDA" "BECDA" "BCEDA" "BCDEA" "BCDAE"
 [91] "BDCAE" "BDCEA" "BDECA" "BEDCA" "EBDCA" "EDBCA" "DEBCA" "DBECA" "DBCEA"
[100] "DBCAE" "DBACE" "DBAEC" "DBEAC" "DEBAC" "EDBAC" "EBDAC" "BEDAC" "BDEAC"
[109] "BDAEC" "BDACE" "BADCE" "BADEC" "BAEDC" "BEADC" "EBADC" "EBACD" "BEACD"
[118] "BAECD" "BACED" "BACDE"
Now, let's get the 3-letter permutation from the same set ("ABCDE").
# The number of the subset (3) permutations.
factorial(5)/factorial(5-3)
[1] 60
# The subset permutations.
subSetPermutations("ABCDE",3)
 [1] "ABC" "ABD" "ABE" "ACB" "ACD" "ACE" "ADB" "ADC" "ADE" "AEB" "AEC" "AED"
[13] "BAC" "BAD" "BAE" "BCA" "BCD" "BCE" "BDA" "BDC" "BDE" "BEA" "BEC" "BED"
[25] "CAB" "CAD" "CAE" "CBA" "CBD" "CBE" "CDA" "CDB" "CDE" "CEA" "CEB" "CED"
[37] "DAB" "DAC" "DAE" "DBA" "DBC" "DBE" "DCA" "DCB" "DCE" "DEA" "DEB" "DEC"
[49] "EAB" "EAC" "EAD" "EBA" "EBC" "EBD" "ECA" "ECB" "ECD" "EDA" "EDB" "EDC"
Notice that the number of the permutation has been reduced by the number of ways the remaining letters can be arranged (here 2! = 2). For example, the first subset permutation ("ABC") has 2 corresponding full set permutations ("ABCDE","ABCED" ) because the letters that are not included in this subset permutation can be arranged in 2! = 1 · 2 = 2 ways.

Now, let's get the 3-letter combination from the same set ("ABCDE").
# The number of the combinations.
factorial(5)/(factorial(5-3)*factorial(3))
[1] 10
# The combinations.
combs("ABCDE",3)
[1] "ABC" "ABD" "ABE" "ACD" "ACE" "ADE" "BCD" "BCE" "BDE" "CDE"
As we can see, the number of the combination is 6 times lower (60 / 10) than the number of the subset permutations. For each combination of 3 letters there are 3! = 1 · 2 · 3 = 6 ways the letters can be arranged in. For example, combination "ABC" has 6 permutations "ABC", "ACB", "BAC", "BCA", "CAB", "CBA".
Examples - Combinations:
Problem 1:
What is the number of outcomes of the MegaBucks Lottery?
# The count of the number set (1,2,...,49) to choose from:
n = 49
# The size of one bet (the count of the number set chosen by a lottery customer):
m = 6
# The number of all possible bets (cnk). This is the number of the combinations of 6 numbers selected from the set of 49 numbers.
cnk = factorial(n)/(factorial(n-m)*factorial(m))
cnk
[1] 13983816
So, there are 13,983,816 possible outcomes and only one of them is the big MegaBucks winner.

Problem 2:
What is the number of outcomes of the PowerBall Lottery?
# The count of the initial number set (1,2,...,69) to choose from:
n1 = 69
# The size of the main bet (the count of the initial set chosen by a lottery customer):
m1 = 5
# The count of the additional number set (1,2,...,26) to choose from:
n2 = 26
# There is just 1 number to be selected from the additional set.
m2 = 1
The number of all possible bets (cnk). This is the product of the number of the combinations of 5 numbers selected from the set of 69 numbers and the number of the possible one-number selections from the additional set of size 26.
Notice that we apply here two counting rules: Product and Combinations.
PowerBallPower = C(69,5) · C(26,1) = C(69,5) · 26
cnk = factorial(n1)/(factorial(n1-m1) * factorial(m1)) * factorial(n2)/(factorial(n2-m2) * factorial(m2))
cnk
[1] 292201338
So, there are 292,201,338 possible outcomes and only one of them is the big PowerBall winner.
 
Power Set
How many different subsets can be selected from a set of n elements?
2n
Consider a set consisting of no elements (n = 0). This set has just one element. It is interpreted as an empty set (∅) which, in the context of probability, is interpreted as an impossible event. A set, consisting of one element (n = 1), has two subsets (here elements). They are the element itself and the empty set (element). Using a combination notation, C(n, m), standing for the number of the combinations of m elements selected from a set of n elements, we can figure out the number of possible subsets of an n-element set as. With a set of 3-elements (n = 3), the all possible subset consist of an empty set, 1-element subsets, 2-element subsets, and 3-element subsets. If we count them, we will get C(3, 0) + C(3, 1) + C(3, 2) + C(3, 3). Let's list a few examples for n = 0,1,2, and 3:
n = 0: C(0,0) = 1
n = 1: C(1,0) + C(1,1) = 1 + 1 = 2
n = 2: C(2,0) + C(2,1) + C(2,2) = 1 + 2 + 1 = 4
n = 3: C(3,0) + C(3,1) + C(3,2) + C(3,3) = 1 + 3 + 3 + 1= 8
The numbers form the so call Pascal's triangle, containing coefficients of the binomial formula [Binomial Theorem].
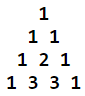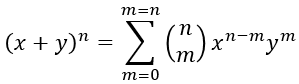Paskal'e Triangle Binomial Formula  where Combinations is the number of the combination of m elements selected
from a set of n elements. This is a cool notation for C(n, m).
In the Pascal's triangle, all the external numbers are equal to 1 and each internal number in row m is the sum of the two closest neighbors in the preceding row (m -1).
If we expand the above formula (without the Σ), we will see better how to combinatorial coefficients develop counts of the m- element subsets of the n-element set.
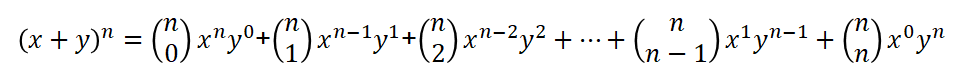
Bonomial
In order to add up just the combinatorial elements, all we need is to set x and y to 1. The formula gets reduced to the following one.
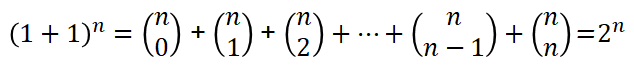
Binomial - Power Set
This confirms the the total number of subsets that can be produced from an n-element set is 2n.
Example - Power Set:
Since events can be interpreted as sets, we can find out how many possible events can be generated by a single roll of a die. The answer is 26 = 64. It would be boring to list them all. To name just a few:
Rolling Die Power Set
Each event is defined between braces "{" and "}".
 
Exercises:
1. In how many ways one can set up tuxedos for a wedding event given the following options: 3 suits, 4 vests, 3 ties, and 5 hats?show
There are n1 = 3 suits, n2 = 4 vests, n3 = 3 ties, and n4 = 5 hats.
Using the Product Rule, the total number of tuxedo sets is the product of the option numbers of the components. n = n1 · n2 · n3 · n4 = 3 · 4 · 3 · 5 · = 180
2. There are 5 students sitting in a row. In how many ways can the student be arranged?show
Using the Full-set Permutation rule, the total number of the arrangements of n = 5 members is n! = 1 · 2 · 3 · 4 · 5 = 120
3. Find out in how many ways can teams of 2 players be arranged from the full set of 5 players.show
Suppose that the full set of the players includes {Ben, Jim, Ken, Ron, Tom}. According to the Subset Permutations rule, the number of the permutations of (m = 2) elements selected from an (n = 5) element set is: 5!/((5-2)!) = 120/6 = 20. Here is a solution in R.
# Open library "iterpc".
library(iterpc)
# The vector of players.
x = c('Ben', 'Jim', 'Ken', 'Ron', 'Tom')
# The number of the players.
n = length(x)
# The size of the teams.
m = 2
# Create an iterator fo the n by n subset permutations.
itr = iterpc(n, m, replace=FALSE, ordered=TRUE)
# Get the permuations as a numeric matrix sp.
sp = getall(itr)
sp
      [,1]  [,2]
 [1,]    1    2
 [2,]    1    3
 [3,]    1    4
 [4,]    1    5
 [5,]    2    1
 [6,]    2    3
 [7,]    2    4
 [8,]    2    5
 [9,]    3    1
[10,]    3    2
[11,]    3    4
[12,]    3    5
[13,]    4    1
[14,]    4    2
[15,]    4    3
[16,]    4    5
[17,]    5    1
[18,]    5    2
[19,]    5    3
[20,]    5    4
# Map the numeric matrix to the names of the players.
structure(x[sp], .Dim = dim(sp))
      [,1]  [,2]
 [1,] "Ben" "Jim"
 [2,] "Ben" "Ken"
 [3,] "Ben" "Ron"
 [4,] "Ben" "Tom"
 [5,] "Jim" "Ben"
 [6,] "Jim" "Ken"
 [7,] "Jim" "Ron"
 [8,] "Jim" "Tom"
 [9,] "Ken" "Ben"
[10,] "Ken" "Jim"
[11,] "Ken" "Ron"
[12,] "Ken" "Tom"
[13,] "Ron" "Ben"
[14,] "Ron" "Jim"
[15,] "Ron" "Ken"
[16,] "Ron" "Tom"
[17,] "Tom" "Ben"
[18,] "Tom" "Jim"
[19,] "Tom" "Ken"
[20,] "Tom" "Ron"
# The above structure statement does the same as the following code.
spc = factorial(5)/factorial(5-2)
for (r in 1:spc) {
  for (c in 1:m) {
     i = sp[r,c]
     subsetPermutations[r,c] = x[i]
  }
}
subsetPermutations
      [,1]  [,2]
 [1,] "Ben" "Jim"
 [2,] "Ben" "Ken"
 [3,] "Ben" "Ron"
 [4,] "Ben" "Tom"
 [5,] "Jim" "Ben"
 [6,] "Jim" "Ken"
 [7,] "Jim" "Ron"
 [8,] "Jim" "Tom"
 [9,] "Ken" "Ben"
[10,] "Ken" "Jim"
[11,] "Ken" "Ron"
[12,] "Ken" "Tom"
[13,] "Ron" "Ben"
[14,] "Ron" "Jim"
[15,] "Ron" "Ken"
[16,] "Ron" "Tom"
[17,] "Tom" "Ben"
[18,] "Tom" "Jim"
[19,] "Tom" "Ken"
[20,] "Tom" "Ron"
# Notice that variable spc, produced above, holds the numbe of the subset permutations.
sp
[1] 20
4. Mass Cash is a popular lottery in Massachusetts. It draws 5 out of 35 numbers. What is the probability of winning the Jackpot (e.g. $100,000)?show
The probability is 1/w, where w is the number of the combinations of (m=5) numbers selected from a set of (n=35) numbers. According to the Combinations rule, the number of the combinations, w, is 35!/((35-5)!·5!) = 324,632. The Jackpot probability is p = 1/w = 1/324,632 = 0.00000308. Here is a solution in R.
# The number of all the lottery numbers.
n = 35
# The size of the lottery bet.
m = 5
# The number of the combination of 5-number sequences selected from the sequence of 35 numbers (1, 2, 3, ..., 35).
w = factorial(n)/(factorial(n-m)*factorial(m))
w
[1] 324632
# The probability of hitting Jackpot.
p = 1/w
# Show the probability with 8 digits after the decimal period.
ps = sprintf("%.8f",p)
ps
[1] "0.00000308"
# Show this result as a decimal numer (function sprintf produces a string).
options("scipen"=100)
p
[1] 0.000003080411
5. How many events (subsets) can be produced from a sample of the coin sides, {Heads, Tails}.show
According to the Power Set rule, one can select 2n subsets from a set consisting of n elements. Since set {Heads, Tails} consists of two elements, the answer is 22 = 4. Here is a simple solution in R.
# The sample space (set).
coin = c("Heads","Tails")
# The size sample space (set).
n = length(coin)
# The total number os all possible events (subsets).
w = 2^n
w
[1] 4
By the way, the events are:
∅
{Heads}
{Tails}
{Heads, Tails}
Spreadsheet Solutions?show
Download: Excel Workbook
Glossary
Product Rule - if there are n instances of entity N and m instances of entity M, then there are n · m instances of both the entities..
Permutations - the number of ways a set of elements can be arranged.
Combinations - the number of unique subsets of size m that can be selected from a set of unique elements size n.
Power Set - a collection of all possible subsets of a set, including a Null subset (∅).
References:
Combinatorial Mathematics
Wikipedia - Rule of Product
Wikipedia - Permutations
Wikipedia - Combinations
Wolfram MathWorld. - Power Set