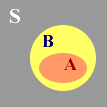
Random Events
A random event is an outcome of a random experiment (a replicable procedure performed under the same conditions).
For example, in an experiment of Flipping a Coin, one of the two events will occur: "Heads" or "Tails".
When Rolling a Die, one can define numerous events such as getting: "an odd number", "a number greater than 2", "one or six", etc.
In Measuring MPG (Miles per Gallon), events like "MPG below 20", "MPG between 20 and 30" or "MPG above 30" may occur.
Although one defines an event that can be satisfied by many different outcomes of an experiment,
what actually comes out from the experiment is a simple event.
For example, an event of getting an odd number in a Single Roll of a Die can materialize as 1, 3, or 5.
Getting any number in this experiment can be satisfied by one of the numbers 1 through 6.
Each of the outcomes (1, 2, 3, 4, 5, 6) is referred to as a simple or elementary event.
Any event can be thought of as a combination of zero, one, many, or all simple events.
An event that has nothing to do with any of the simple events is called an impossible event (∅).
For example, in a Single Roll of a Die, getting a number that is even and odd is impossible.
Any number (outcome) must be either even or odd but not both. Using a set notation we can formulate such an event as {2,4,6} ∩ {1,3,5} = ∅. On the other hand, an event that can be satisfied by any of the simple events is called a certain event (S).
For example getting an odd or even number, in the same experiment, is certain since there are no other numbers (only even or odd).
Using a set notation we can formulate such an event as {2,4,6} ∪ {1,3,5} = S. 
There is an interesting and useful analogy between events and sets. One can think of a simple event as of an element of a set.
The sample space and certain event would then be equivalent to the [whole] set, S. An impossible event could be represented by an empty
set, ∅. An event, X, that can be satisfied by more than one simple event is interpreted as a subset of set S, X ⊆ S. Such an event is also referred to as a compound event. More importantly, all basic set operations can also be applied to events.
Set notations are frequently used to represent and manipulate events. Simple events are symbolized by lower-case letters and a compound
events—by capital letters. A capital letter S usually stands for the sample space (certain event). Using the set notations one can conveniently defined more
complex events and their properties.
An event Z is a union
of events X or Y, Z = X ∪ Y, if Z consists of events that satisfy X or Y. (Notice that, in plain English, we could say Z is a union
of events X and Y. However, conjunctive word and may be misleading here as it is used logically to formulate intersections. This is why this union is expressed as "X or Y" even so it may not sound well "language-wise".)
For example, when Rolling a Die, let X = {1, 2, 3} and Y={3, 4}. Union X or Y = {1, 2, 3, 4}. This union includes all events (elements) that satisfy (belong to) X plus (or) those that belong to Y. Notice that event {3} belongs to both X and Y. However, in a union, each element appears only once. The following are common properties of the union:
For example, when Rolling a Die, let X = {1, 2, 3} and Y={3, 4}. Union X or Y = {1, 2, 3, 4}. This union includes all events (elements) that satisfy (belong to) X plus (or) those that belong to Y. Notice that event {3} belongs to both X and Y. However, in a union, each element appears only once. The following are common properties of the union:
X ∪ Y = Y ∪ X
X ∪ ∅ = X
X ∪ X = X
X ∪ S = S
X ∪ (Y ∪ Z) = X ∪ Y ∪ Z = (X ∪ Y) ∪ Z
A ⊆ B ⇔ A ∪ B = B (where ⇔ stands for "if and only
if") 
An event Z is an intersection of events X and Y, Z = X ∩ Y, if Z consists of events that simultaneously
satisfy X and Y. As mentioned, the common notation for this operation is X ∩ Y. For example, when Rolling a Die,
let X = {2, 4, 6} and
Y = {3, 4, 5}. Intersection X ∩ Y = {4}. This intersection includes all events (here event) that satisfy (belong to) both X and Y. It is simply an overlap of these events. The following are common properties of the intersection:
Y = {3, 4, 5}. Intersection X ∩ Y = {4}. This intersection includes all events (here event) that satisfy (belong to) both X and Y. It is simply an overlap of these events. The following are common properties of the intersection:
X ∩ Y = Y ∩ X
X ∩ ∅ = ∅
X ∩ X = X
X ∩ S = X
X ∩ (Y ∩ Z) = X ∩ Y ∩ Z = (X ∩ Y) ∩ Z
X ∩ (Y ∪ Z) = X ∩ Y ∪ X ∩ Z

A ⊆ B ⇔ A ∩ B = A
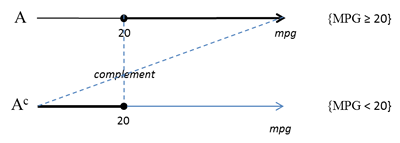
Complement of an Event
Event Xc is said be a complement of event X if it satisfies those simple events from the sample space,
S, that do not satisfy event X. Other common notations for Xc are X', ¬X, or not X.
More explicit definition shows that the complement of event X is the difference between the sample space, S, and the event: Xc = S \ X (where \ stands for set-operator minus).
For example, when Rolling a Die, let X = {2, 4, 6}. Recall that sample space, S, consists of elements (simple events)
{1, 2, 3, 4, 5, 6}. Complement of X, Xc = {1,3,5}. Notice that Xc is just the difference between S and X, {1, 3, 5} = {1, 2, 3, 4, 5, 6} \ {2, 4, 6}. It includes those events from S that are not in X. One can also say that Xc is a negation of X with respect of space S. The following are common properties of the complement:
For example, when Rolling a Die, let X = {2, 4, 6}. Recall that sample space, S, consists of elements (simple events)
{1, 2, 3, 4, 5, 6}. Complement of X, Xc = {1,3,5}. Notice that Xc is just the difference between S and X, {1, 3, 5} = {1, 2, 3, 4, 5, 6} \ {2, 4, 6}. It includes those events from S that are not in X. One can also say that Xc is a negation of X with respect of space S. The following are common properties of the complement:
X ∪ Xc = S 
X ∩ Xc = ∅ 
Sc = ∅ 
∅c = S 
De Morgan's Laws:
There are interesting relationships between the three basic event (set) operations: union,
interaction and complement. They are captured by two famous De Morgan's Laws::
1. The complement of an intersection of two events is equivalent (≡) to the union of the complements of the events.
(X ∩ Y)c ≡ Xc ∪ Yc
2. The complement of a union of two events is equivalent (≡) to the intersection of the complements of the events.
(X ∪ Y)c ≡ Xc ∩ Yc
Examples:
Let X = {1,2,3,4}, Y = {3,4,5,6} in a sample space S = {1,2,3,4,5,6}.
1. Show that L = (X ∩ Y) c ≡ Xc ∪ Yc = R (here L stands for the left size, and R stands for the right side).
X ∩ Y = {1,2,3,4} ∩ {3,4,5,6} = {3,4}
L = (X ∩ Y) c = {1,2,5,6}
Xc = {1,2,3,4}c = {5,6}
Yc = {3,4,5,6}c = {1,2}
Xc ∪ Yc = {5,6} ∪ {1,2} = {1,2,5,6) = R
Thus L = R
2. Let's show that L = (X ∪ Y) c ≡ Xc ∩ Yc = R
X ∪ Y = {1,2,3,4} ∪ {3,4,5,6} = {1,2,3,4,5,6} = S
L = (X ∪ Y)c = Sc = ∅
Xc ∩ Yc = {5,6} ∩ {1,2} = ∅ = R
Thus L = R
Exercises:
1. Consider an experiment of Flipping Two Fair Coins. What is the sample space (the set of all simple events), S, of this experiment? 
2. In Flipping Two Fair Coins, event X = {HT,TH}. What is the complement of this event, Xc?

3. For an experiment of Rolling a Die, assume event A = {1, 3, 5} (an odd number), B = {2, 4, 6} (an event number), and
C = {1, 4, 6}. Find out the following compound events:
C = {1, 4, 6}. Find out the following compound events:
a) A ∩ B =

b) Ac =

c) A ∪ C =

d) A ∩ C =

e) C ∩ A ∪ B =

f) C ∩ (A ∪ B) =

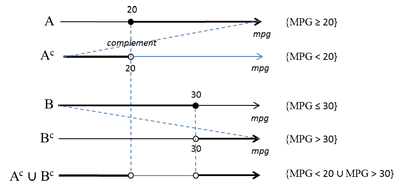
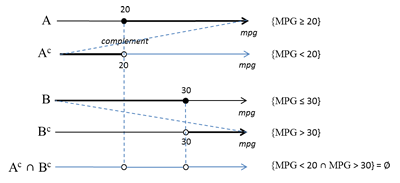
4. In an experiment of Measuring Miles Per Gallon, group A of cars accomplished results of at least 20 mpg and group B made up to 30 mpg.
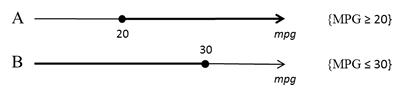
Given event A includes all the results of group A, A = {MPG≥20}, and event B includes the results of group B,
B ={MPG≤30}, evaluate the following compound events:

Given event A includes all the results of group A, A = {MPG≥20}, and event B includes the results of group B,
B ={MPG≤30}, evaluate the following compound events:
a) A ∩ B =

b) A ∪ B =

c) Ac =

d) Ac ∪ Bc =

e) Ac ∩ Bc =

Implementation
Examples and Exercises for Random Events Implemented as R Sets
R can handle set operations, using the following functions:
- union(setA, setB) for evaluation of setA ∪ setB
- intersect(sement_xetB) for evaluation of setA ∩ setB
- setdiff(setA, setB) for evaluation of setA \ setB
- setequal(setA, setB) for evaluation of setA ≡ setB
- is.element(element_x, setX), which is equivalent to element_x %in% setX for evaluation of element_x ∈ setX
Examples
1. Sample space for expriment "Rolling a Die" expressed as a set.
S = 1:6 # same as, in Math, S = {1,2,3,4,5,6}
print(S)
print(S)
[1] 1 2 3 4 5 6
2. A Union of events.
Asume the following sets: A = {1,3,5}, B = {3,4}
Asume the following sets: A = {1,3,5}, B = {3,4}
A = c(1,3,5)# c() is an R function used to construct simple collections.
B = c(3,4) # Here such a collection is called a vector.
AorB = union(A, B)
print(AorB) # Notice that element 3 is accounted for one time.
B = c(3,4) # Here such a collection is called a vector.
AorB = union(A, B)
print(AorB) # Notice that element 3 is accounted for one time.
[1] 1 3 5 4
3. An Intersection of events.
Let A = {1,3,5} and B = {3,4}.
Let A = {1,3,5} and B = {3,4}.
A = c(1,3,5)
B = c(3,4)
AandB = intersect( A, B)
print(AandB)
B = c(3,4)
AandB = intersect( A, B)
print(AandB)
[1] 3
4. A difference between events.
Let A = {1,3,5} and B = {3,4}
Let A = {1,3,5} and B = {3,4}
A = c(1,3,5)
B = c(3,4)
AminusB = setdiff(A, B)
cat(AminusB) # Notice a slight difference between the previous print() result and this cat() outcome.
B = c(3,4)
AminusB = setdiff(A, B)
cat(AminusB) # Notice a slight difference between the previous print() result and this cat() outcome.
1 5
5. A complement of an event.
S = {1,2,3,4,5,6}, A = {1,3,5}
Show the complement of event (set) A in space S.
S = {1,2,3,4,5,6}, A = {1,3,5}
Show the complement of event (set) A in space S.
S = 1:6 # The sample space in "Rolling a Die"
A = c(1,3,5)
ComplementOfA = setdiff(S, A)
# A more descriptive printout:
cat('Complement of A in S is {',ComplementOfA,'}\n')
cat('Notice:\n')
cat(' S = {',S,'}\n')
cat(' A = {',A,'}\n')
A = c(1,3,5)
ComplementOfA = setdiff(S, A)
# A more descriptive printout:
cat('Complement of A in S is {',ComplementOfA,'}\n')
cat('Notice:\n')
cat(' S = {',S,'}\n')
cat(' A = {',A,'}\n')
Complement of A in S is {2 4 6}
Notice:
S = {1 2 3 4 5 6}
A = {1 3 5}
6. Maintaining uniqueness of the set elements.
Let A = {1,1,1,4,4,6} and B = {2,2,2}
Get the union of sets A, B.
Let A = {1,1,1,4,4,6} and B = {2,2,2}
Get the union of sets A, B.
A = c(1,1,1,4,4,6)
B = c(2,2,2)
AorB = union(A, B)
cat('Union of A, B = {'); cat(AorB); cat('}\n')
cat('Notice:\n')
cat(' A = {'); cat(A); cat('}\n')
cat(' B = {'); cat(B); cat('}\n')
B = c(2,2,2)
AorB = union(A, B)
cat('Union of A, B = {'); cat(AorB); cat('}\n')
cat('Notice:\n')
cat(' A = {'); cat(A); cat('}\n')
cat(' B = {'); cat(B); cat('}\n')
Union of A, B is {1 4 6 2}
Notice:
A = {1 1 1 4 4 6}
B = {2 2 2}
Notice that the order of elements is sets is irrelevant. Since sets are stored in R vectors, one can sort also the sets. For example:
print(sort(setAorB))
[1] 1 2 4 6
Exercises
1. Consider an experiment of Flipping Two Fair Coins. What is the sample space (the set of all simple events), S, of this experiment?

2. In Flipping Two Fair Coins, event X = {HT,TH}. Find out the sample spacs, S, and the complement of event X, Xc?

The above exercise uses function print() that requires the print content to be combined into one object. It is accomplished by means of the paste() function that combines print items separated (by default) with a space. Some of the items are sets. The elements of the sets are concatenated also using the paste() function. They are collapsed into strings, heving individual items separated with a comma and space (', '). Thanks to argument quote=FALSE, these print operations show unquoted output.
A similar output format can be produced, using function cat().
A similar output format can be produced, using function cat().
cat('Sample space, S = { '); cat(paste(S, collapse=', ')); cat(' }\n')
cat('Event, X = { '); cat(paste(X, collapse=', ')); cat(' }\n')
cat('Complement of X in S = { '); cat(paste(comp_of_X, collapse=', ')); cat(' }')
cat('Event, X = { '); cat(paste(X, collapse=', ')); cat(' }\n')
cat('Complement of X in S = { '); cat(paste(comp_of_X, collapse=', ')); cat(' }')
Sample space, S = { HT, HH, TH, TT }
Event, X = { HT, TH }
Complement of X in S is { HH, TT }
Notice how convenient the paste() function is when dealing with complex data structures (here—with vectors). The following example compares two methods of getting the same printout.
# Method 1
cat(paste(S, collapse=', '),'\n')
# Method 2
for (i in 1:(length(S)-1)) {
cat(S[i],', ',sep='')
}
cat(S[length(S)])
cat(paste(S, collapse=', '),'\n')
# Method 2
for (i in 1:(length(S)-1)) {
cat(S[i],', ',sep='')
}
cat(S[length(S)])
HT, HH, TH, TT HT, HH, TH, TT
The second method uses a for loop to iterate over the elements of set (vector) S. Each element, S[i], is printed by the cat() function. Inside the loop (between { and }), the elements are followed by a comma and space (', ') with no other separator (sep=''). The last element is printed alone outside the loop. Obviously, Method 1 is much simpler and productive.
3. For an experiment of Rolling a Die, assume event A = {1, 3, 5} (an odd number), B = {2, 4, 6} (an event number), and C = {1, 4, 6}. Find out the following compound events:
3a: A ∩ B =
3a: A ∩ B =
3b: Ac = (with respect to the sample space)

3c: A ∪ C =

3d: A ∩ C = 
3f: C ∩ (A ∪ B) =

4. In an experiment of Measuring Miles Per Gallon, group A of cars accomplished results of at least 20 mpg and group B made up to 30 mpg. Using the interval notation the sets can be defined mathematically as A = [20,∞) and B = (-∞,30].

Standard R does not have proper functions to handle [interval] sets of continuous variables. However, library sets provides interesting functions to perform set operations on continuous intervals. While in R, first install the library (package) sets:

Standard R does not have proper functions to handle [interval] sets of continuous variables. However, library sets provides interesting functions to perform set operations on continuous intervals. While in R, first install the library (package) sets:
install.packages('sets')
If you are installing this package for another R distribution, for example, for Anaconda, first find the installation "Home" of this installation and locate its R library folder. On the author's system, the installation's target folder (R_Library_Path) is 'C:/bisoft/anaconda/Lib/R/library'. Finally, run the installation with the path to this library:
install.packages('sets','R_Library_Path')
Upon success, declare the library and apply its functions.
4a: A ∩ B =
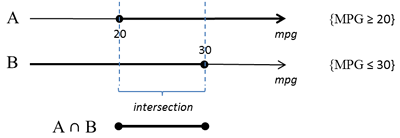
4b: A ∪ B =
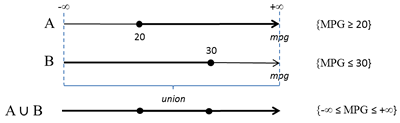
4c: Ac =
4d: Ac ∪ Bc =
4e: Ac ∩ Bc =
Examples and Exercises for Random Events Implemented as Spreadsheet Sets
Spreadsheet program (e.g. Excel, Google Sheets, Apple Numbers, etc.) do not have built-in set operations (functions or procedures). Elements of sets can be stored in spreadsheet ranges of cells, resembling R vectors. The following functions can be useful in performing set operations (unions, intersections, differences).
- MATCH(e, x, 0) for checking if element e belongs to set x (0 stands of an exact match).
- COUNTIF(x, e) for checking if element e belongs to set x (result 0 indicates the e ∉ x, result > 0 shows that e ∈ x).
The above functions do not perform the set operations alone. Other functions are needed in order to properly interpret the outcomes of the MATCH() and COUNTIF() functions.
Function call MATCH(e, x, 0) returns the position (index) of element (cell) e in range x or #N/A if the element does not exist. The set operations (unions, intersections, differences) require that the [tested] element or "empty" (null) set is returned which can be done by embedding the MATCH() function in other functions. Logically, one could say that if the MATCH(e, x, 0) call returns #N/A then the resulting set gets an empty element (""), otherwise the set gets element e. One can use function IF() to perform such a query. However, the function's test may not directly compare the ouctome of function MATCH() to #N/A. This can be done by function ISNA() which returns TRUE if its argument is equal to #N/A or FALSE otherwise. The final solution to this problem requires double embeddingof the MATCH() function: =IF(ISNA(MATCH(e,x,0)),"",e).
Function COUNTIF() is somewhat easier to handle. A direct call COUNTIF(x, e) returns 0 (zero) if element e does not exist in range x, or the number of times element e appears in range x (with range x containing unique values, element e may be there at most one time). Thus, in this case, the COUNTIF() function can be directly embedded in the IF() function: =IF(COUNTIF(x, e)=0,"",e).
Examples
1. Use function MATCH() to compute the Union, Intersection, and Differences for sets A and B defined in the following spreadsheet.
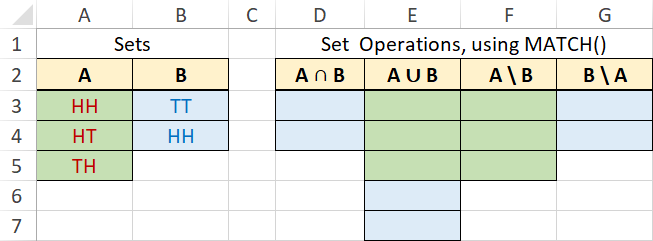
Check the solution at Set Operations, Using Google Sheets (Worksheet SetOpsWithMatch).
Formulas:
Formulas:
D3: =IF(ISNA(MATCH(B3,$A$3:$A$5,0)),"",B3) D4: Copy D3 to D4 E3: =A3 E4,E5: Copy E3 to E4:E5 E6: =IF(ISNA(MATCH(B3,$A$3:$A$5,0)),B3,"") E7: Copy E6 to E7 F3: =IF(ISNA(MATCH(A3,$B$3:$B$4,0)),A3,"") F4,F5: Copy F3 to F4:F5 G3: =IF(ISNA(MATCH(B3,$A$3:$A$5,0)),B3,"") G4: Copy G3 to G4
2. Use function COUNTIF() to compute the Union, Intersection, and Differences for sets A and B defined in the following spreadsheet.
Check the solution at Set Operations, Using Google Sheets (Worksheet SetOpsWithCountIf).
Formulas:
Formulas:
D3: =IF(COUNTIF($A$3:$A$5,B3)=1,B3,"") D4: Copy D3 to D4 E3: =A3 E4,E5: Copy E3 to E4:E5 E6: =IF(COUNTIF($A$3:$A$5,B3)=1,"",B3) E7: Copy E6 to E7 F3: =IF(COUNTIF($B$3:$B$4,A3)=1,"",A3) F4,F5: Copy F3 to F4:F5 G3: =IF(COUNTIF($A$3:$A$5,B3)=1,"",B3) G4: Copy G3 to G4
Exercises
1. Compute the Union, Intersection, and Differences for the following data sets (A, B), using function MATCH().
| A | B | C | D | E | F | G | |
| 1 | Sets | Set Operations, using function MATCH() | |||||
| 2 | X | Y | X ∩ Y | X ∪ Y | X \ Y | X \ Y | |
| 3 | blue | orange | |||||
| 4 | cyan | black | |||||
| 5 | orange | grey | |||||
| 6 | magenta | red | |||||
| 7 | red | ||||||
| 8 | green | ||||||
Hint: Copy the above table to a spreadsheet and use formulas similar to those shown in Example 1.
2. Compute the Union, Intersection, and Differences for the following data sets (A, B), using function COUNTIF().
| A | B | C | D | E | F | G | |
| 1 | Sets | Set Operations, using function COUNTIF() | |||||
| 2 | X | Y | X ∩ Y | X ∪ Y | X \ Y | X \ Y | |
| 3 | blue | orange | |||||
| 4 | cyan | black | |||||
| 5 | orange | grey | |||||
| 6 | magenta | red | |||||
| 7 | red | ||||||
| 8 | green | ||||||
Hint: Copy the above table (without the top row and left column) to a spreadsheet and use formulas similar to those shown in Example 2.
Glossary
Random Experiment - a replicable procedure performed under the same conditions, returning a random outcome.
Simple Event - the actual outcome of a random experiment (an element of a set).
Sample Space - the collection of all simple events (the entire set the elements, each representing one simple event).
Random Event - an outcome of a Random Experiment (a subset of the set). Also referred to as a compound event.
Certain Event - an event equivalent to the Sample Space. It is said to occur for sure.
Impossible Event - an event opposite to the Certain Event (equivalent to an empty set). It will never occur.
Union of Events - event Z is a union of events A, B, Z = A ∪ B, if Z includes simple events from A or B.
Intersection of Events - event Z is an intersection of events A, B, Z = A ∩ B, if for each simple event in Z the event exists in both A and B.
Event Complement - event A is a complement of event B, A = Bc, if for each simple event in A, the event does not exist in B.
References: